"

Learning Objectives

In this section, you will:

  • Determine proper interval notation
  • Find the domain of a function defined by an equation.
  • Find the domain of a function defined by a graph.

 

In this section, we will practice determining domains and ranges for specific functions. Keep in mind that, in determining domains and ranges, we need to consider what is physically possible or meaningful in real-world examples. We also need to consider what is mathematically permitted. For example, we cannot include any input value that leads us to take an even root of a negative number if the domain and range consist of real numbers. Or in a function expressed as a formula, we cannot include any input value in the domain that would lead us to divide by 0. We can visualize the domain as a “holding area” that contains “raw materials” for a “function machine” and the range as another “holding area” for the machine’s products.

Diagram of how a function relates two relations.

We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded. For example, if a person has \mathdollar 100 to spend, he or she would need to express the interval that is more than 0 and less than or equal to 100 and write \left(0,100\right] . We will discuss interval notation in greater detail later.

Let’s turn our attention to finding the domain of a function whose equation is provided. Oftentimes, finding the domain of such functions involves remembering three different forms. First, if the function has no denominator or an even root, consider whether the domain could be all real numbers. Second, if there is a denominator in the function’s equation, exclude values in the domain that force the denominator to be zero. Third, if there is an even root, consider excluding values that would make the radicand negative.

Before we begin, let us review the conventions of interval notation:

  • The smallest number from the interval is written first.
  • The largest number in the interval is written second, following a comma.
  • Parentheses, ( or ), are used to signify that an endpoint value is not included, called exclusive.
  • Brackets, [ or ], are used to indicate that an endpoint value is included, called inclusive.

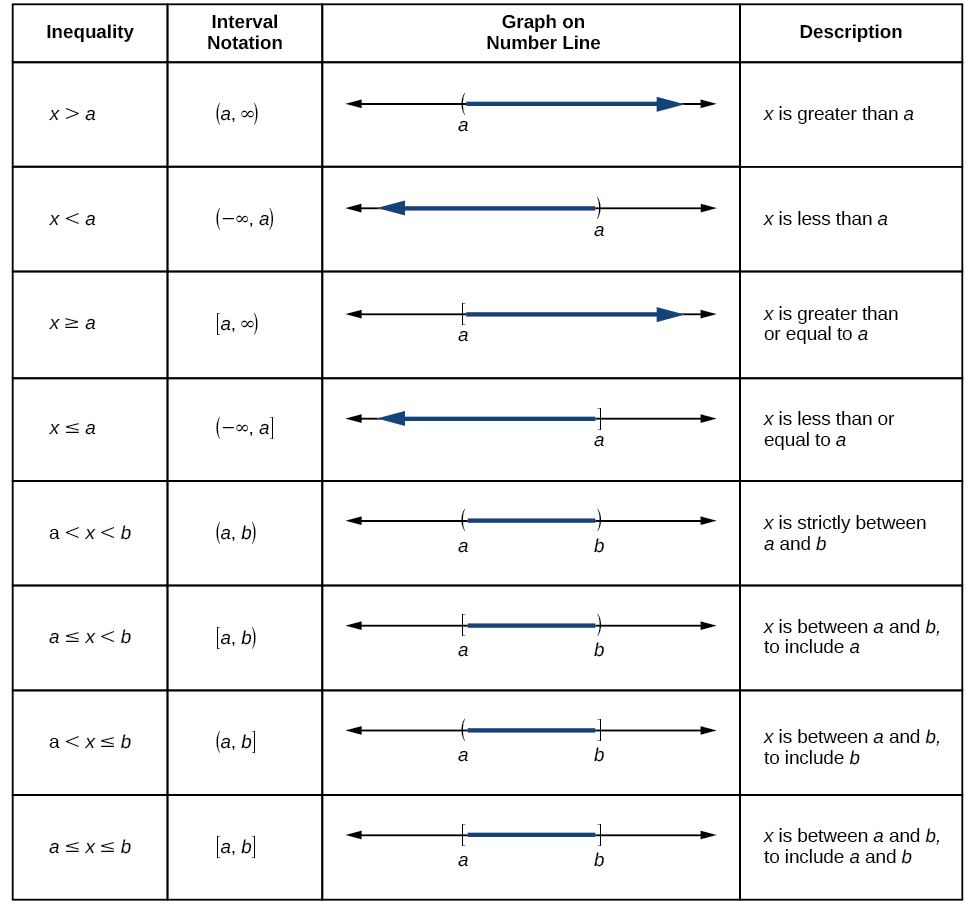
Summary of interval notation.

Finding the Domain of a Function as a Set of Ordered Pairs

Find the domain of the following function: \left{\left(2,10\right), \left(3,\right), \left(4, 20\right), \left(5, 30\right), \left(6,40\right)\right} .

Show Solution

First identify the input values. The input value is the first coordinate in an ordered pair. There are no restrictions, as the ordered pairs are simply listed. The domain is the set of the first coordinates of the ordered pairs.

\left{2,3,4,5,6\right}

How To

Given a function written in equation form, find the domain.

  1. Identify the input values.
  2. Identify any restrictions on the input and exclude those values from the domain.
  3. Write the domain in interval form, if possible.

Finding the Domain of a Function

Find the domain of the function f\left(x\right)={x}^{2}-1 \

Show Solution

The input value, shown by the variable x in the equation, is squared and then the result is lowered by one. Any real number may be squared and then be lowered by one, so there are no restrictions on the domain of this function. The domain is the set of real numbers.

In interval form, the domain of f is \left(-\infty ,\infty \right) .

Try It

Find the domain of the function: f\left(x\right)=5-x+{x}^{3} .

Show Solution

\left(-\infty ,\infty \right)

Using Notations to Specify Domain and Range

In the previous examples, we used inequalities and lists to describe the domain of functions. We can also use inequalities, or other statements that might define sets of values or data, to describe the behavior of the variable in set-builder notation. For example, left{x|10 \le x<30right} describes the behavior of x in set-builder notation. The braces left{right} are read as “the set of,” and the vertical bar | is read as “such that,” so we would read left{x|10 \le x<30right} as “the set of x-values such that 10 is less than or equal to x, and x is less than 30.”

 

Summary of notations for inequalities, set-builder, and intervals.
Figure 5.

To combine two intervals using inequality notation or set-builder notation, we use the word “or.” As we saw in earlier examples, we use the union symbol, cup to combine two unconnected intervals. For example, the union of the sets left{2,3,5right}
and \left{4,6\right} is the set \left{2,3,4,5,6\right}. It is the set of all elements that belong to one or the other (or both) of the original two sets. For sets with a finite number of elements like these, the elements do not have to be listed in ascending order of numerical value. If the original two sets have some elements in common, those elements should be listed only once in the union set. For sets of real numbers on intervals, another example of a union is

\left{x|text{ }|x|\ge 3\right}=\left(-\infty ,-3\right] \cup \left[3,\infty \right)

Set-Builder Notation and Interval Notation

Set-builder notation is a method of specifying a set of elements that satisfy a certain condition. It takes the form \left{x|, \text{statement about }x\right} which is read as, “the set of all x such that the statement about x is true.” For example,

\left{x|4<x \le 12\right}

Interval notation is a way of describing sets that include all real numbers between a lower limit that may or may not be included and an upper limit that may or may not be included. The endpoint values are listed between brackets or parentheses. A square bracket indicates inclusion in the set, and a parenthesis indicates exclusion from the set. For example,

\left(4,12\right]

Can there be functions in which the domain and range do not intersect at all?

Yes. For example, the function f\left(x\right)=-\dfrac{1}{\sqrt{x}} has the set of all positive real numbers as its domain but the set of all negative real numbers as its range. As a more extreme example, a function’s inputs and outputs can be completely different categories (for example, names of weekdays as inputs and numbers as outputs, as on an attendance chart), in such cases the domain and range have no elements in common.

Finding Domain and Range from Graphs

Another way to identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis. Keep in mind that if the graph continues beyond the portion of the graph we can see, the domain and range may be greater than the visible values.

Graph of a polynomial that shows the x-axis is the domain and the y-axis is the range

We can observe that the graph extends horizontally from -5 to the right without bound, so the domain is \left[-5, \infty \right) . The vertical extent of the graph is all range values 5 and below, so the range is \left(-\infty, 5 \right] . Note that the domain and range are always written from smaller to larger values, or from left to right for domain, and from the bottom of the graph to the top of the graph for range.

Finding Domain and Range from a Graph

Find the domain and range of the function f whose graph is below.

Graph of a function from (-3, 1].

Show Solution

We can observe that the horizontal extent of the graph is –3 to 1, so the domain of f is \left(-3,1 \right] .

The vertical extent of the graph is 0 to –4, so the range is \left[-4,0 \right) .

Graph of the previous function shows the domain and range.

Common Algebraic Domain Restrictions

In general, there are several reasons why the domain of a function will be restricted. We will continue to explore these possibilities as we work with different toolkit functions. There are 3 main reason why the domain of a functions will be restricted:

  1. A value that caused division by zero which will result from a rational function.
  2. A value that has undefined output values that result from a negative argument inside a logarithmic function.
  3. A value that has undefined output values that result from a negative radicand inside an even root power function.

How To

Given the formula for a function, determine the domain and range.

  1. Exclude from the domain any input values that result in division by zero.
  2. Exclude from the domain any input values that have nonreal (or undefined) number outputs.
  3. Use the valid input values to determine the range of the output values.
  4. Look at the function graph and table values to confirm the actual function behavior.

Finding the Domain and Range Using Toolkit Functions

Find the domain and range of f\left(x\right)=2{x}^{3}-x .

Show Solution

There are no restrictions on the domain, as any real number may be cubed and then subtracted from the result.

The domain is \left(-\infty ,\infty \right) and the range is also \left(-\infty ,\infty \right) .

Finding the Domain and Range Using Toolkit Functions

Find the domain and range of f\left(x\right)= \dfrac{2}{x+1} .

Show Solution

We cannot evaluate the function at -1 because division by zero is undefined. The domain is \left(-\infty ,-1\right)cup \left(-1,\infty \right). Because the function is never zero, we exclude 0 from the range. The range is \left(-\infty ,0\right)cup \left(0,\infty \right) .

Finding the Domain and Range Using Toolkit Functions

Find the domain and range of f\left(x\right)=2\sqrt{x+4} .

Show Solution

We cannot take the square root of a negative number, so the value inside the radical must be nonnegative.

x+4 \ge 0 \text{ when }xge -4

The domain of f\left(x\right) is left[-4,\infty \right) .

We then find the range. We know that f\left(-4\right)=0, and the function value increases as x increases without any upper limit. We conclude that the range of f is left[0,\infty \right) .

Graph of a square root function at (-4, 0).

Try It

Find the domain and range of f\left(x\right)=-\sqrt{2-x} .

Show Solution

domain: \left(-\infty ,2 \right]; range: \left(-\infty ,0 \right]

Access these online resources for additional instruction and practice with domain and range.

Key Concepts

  • The domain of a function includes all real input values that would not cause us to attempt an undefined mathematical operation, such as dividing by zero or taking the square root of a negative number.
  • The domain of a function can be determined by listing the input values of a set of ordered pairs.
  • The domain of a function can also be determined by identifying the input values of a function written as an equation.
  • Interval values represented on a number line can be described using inequality notation, set-builder notation, and interval notation.
  • For many functions, the domain and range can be determined from a graph.
  • An understanding of toolkit functions can be used to find the domain and range of related functions.

License

Icon for the Creative Commons Attribution 4.0 International License

MAT 1073 College Algebra Reading Copyright © 2025 by OpenStax is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book