Learning Module 05B Quadratic Equations & Quadratic Functions
Quadratic Functions
Learning Objectives
In this section, you will:
- Recognize characteristics of parabolas.
- Understand how the graph of a parabola is related to its quadratic function.
- Determine a quadratic function’s minimum or maximum value.
- Solve problems involving a quadratic function’s minimum or maximum value.

Curved antennas, such as the ones shown above are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function.
In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Working with quadratic functions can be less complex than working with higher degree functions, so they provide a good opportunity for a detailed study of function behavior.
Recognizing Characteristics of Parabolas
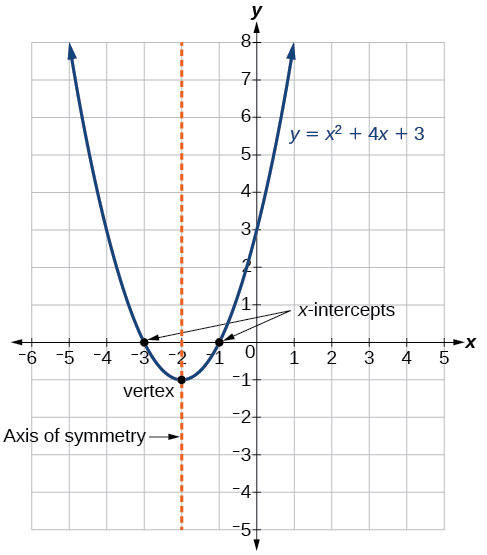
The graph of a quadratic function is a U-shaped curve called a parabola. One important feature of the graph is that it has an extreme point, called the vertex. If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value. In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry.

The y-intercept is the point at which the parabola crosses the y-axis. The x-intercepts are the points at which the parabola crosses the x-axis. If they exist, the x-intercepts represent the zeros, or roots, of the quadratic function, the values of ![]() at which
at which ![]() .
.
Identifying the Characteristics of a Parabola
Determine the vertex, axis of symmetry, zeros, and ![]() intercept of the parabola shown.
intercept of the parabola shown.

Show Solution
The vertex is the turning point of the graph. We can see that the vertex is at ![]() Because this parabola opens upward, the axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is
Because this parabola opens upward, the axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is ![]() This parabola does not cross the
This parabola does not cross the ![]() axis, so it has no zeros. It crosses the
axis, so it has no zeros. It crosses the ![]() axis at
axis at ![]() so this is the y-intercept.
so this is the y-intercept.
Understanding How the Graphs of Parabolas are Related to Their Quadratic Functions
The general form of a quadratic function presents the function in the form
where ![]() and
and ![]() are real numbers and
are real numbers and ![]() If
If ![]() the parabola opens upward. If
the parabola opens upward. If ![]() the parabola opens downward. We can use the general form of a parabola to find the equation for the axis of symmetry.
the parabola opens downward. We can use the general form of a parabola to find the equation for the axis of symmetry.
The axis of symmetry is defined by ![]() If we use the quadratic formula,
If we use the quadratic formula, ![]() to solve
to solve ![]() for the
for the ![]() intercepts, or zeros, we find the value of
intercepts, or zeros, we find the value of ![]() halfway between them is always
halfway between them is always ![]() the equation for the axis of symmetry.
the equation for the axis of symmetry.
The graph below of the quadratic function written in general form as ![]() In this form,
In this form, ![]() and
and ![]() Because
Because ![]() the parabola opens upward. The axis of symmetry is
the parabola opens upward. The axis of symmetry is ![]() This also makes sense because we can see from the graph that the vertical line
This also makes sense because we can see from the graph that the vertical line ![]() divides the graph in half. The vertex always occurs along the axis of symmetry. For a parabola that opens upward, the vertex occurs at the lowest point on the graph, in this instance,
divides the graph in half. The vertex always occurs along the axis of symmetry. For a parabola that opens upward, the vertex occurs at the lowest point on the graph, in this instance, ![]() The
The ![]() intercepts, those points where the parabola crosses the
intercepts, those points where the parabola crosses the ![]() axis, occur at
axis, occur at ![]() and
and ![]() .
.
The standard form of a quadratic function presents the function in the form
where ![]() is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function.
is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function.
As with the general form, if ![]() the parabola opens upward and the vertex is a minimum. If
the parabola opens upward and the vertex is a minimum. If ![]() the parabola opens downward, and the vertex is a maximum. The graph below represents the graph of the quadratic function written in standard form as
the parabola opens downward, and the vertex is a maximum. The graph below represents the graph of the quadratic function written in standard form as ![]() Since
Since ![]() in this example,
in this example, ![]() In this form,
In this form, ![]() and
and ![]() Because
Because ![]() the parabola opens downward. The vertex is at
the parabola opens downward. The vertex is at ![]() .
.

The standard form is useful for determining how the graph is transformed from the graph of ![]() The graph of this basic function.
The graph of this basic function.

If ![]() the graph shifts upward, whereas if
the graph shifts upward, whereas if ![]() the graph shifts downward. In the graph
the graph shifts downward. In the graph ![]() so the graph is shifted 4 units upward. If
so the graph is shifted 4 units upward. If ![]() the graph shifts toward the right and if
the graph shifts toward the right and if ![]() the graph shifts to the left. In the graph,
the graph shifts to the left. In the graph, ![]() so the graph is shifted 2 units to the left. The magnitude of
so the graph is shifted 2 units to the left. The magnitude of ![]() indicates the stretch of the graph. If
indicates the stretch of the graph. If![]() the point associated with a particular
the point associated with a particular ![]() value shifts farther from the x-axis, so the graph appears to become narrower, and there is a vertical stretch. But if
value shifts farther from the x-axis, so the graph appears to become narrower, and there is a vertical stretch. But if ![]() the point associated with a particular
the point associated with a particular ![]() value shifts closer to the x-axis, so the graph appears to become wider, but in fact there is a vertical compression. In the graph,
value shifts closer to the x-axis, so the graph appears to become wider, but in fact there is a vertical compression. In the graph, ![]() so the graph becomes narrower.
so the graph becomes narrower.
The standard form and the general form are equivalent methods of describing the same function. We can see this by expanding out the general form and setting it equal to the standard form.
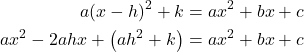
For the linear terms to be equal, the coefficients must be equal.
This is the axis of symmetry we defined earlier. Setting the constant terms equal:
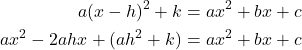
In practice, though, it is usually easier to remember that k is the output value of the function when the input is ![]() so
so ![]() .
.
Forms of Quadratic Functions
A quadratic function is a polynomial function of degree two. The graph of a quadratic function is a parabola.
The general form of a quadratic function is ![]() where
where ![]() and
and ![]() are real numbers and
are real numbers and ![]() .
.
The standard form of a quadratic function is ![]() where
where ![]() .
.
The vertex ![]() is located at
is located at
How To
Given a graph of a quadratic function, write the equation of the function in general form.
- Identify the horizontal shift of the parabola; this value is
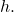 Identify the vertical shift of the parabola; this value is
Identify the vertical shift of the parabola; this value is 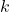 .
. - Substitute the values of the horizontal and vertical shift for
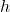 and
and 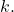 in the function
in the function 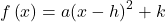 .
. - Substitute the values of any point, other than the vertex, on the graph of the parabola for
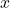 and
and  .
. - Solve for the stretch factor,
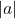 .
. - Expand and simplify to write in general form.
Writing the Equation of a Quadratic Function from the Graph
Write an equation for the quadratic function ![]() as a transformation of
as a transformation of ![]() and then expand the formula, and simplify terms to write the equation in general form.
and then expand the formula, and simplify terms to write the equation in general form.

Show Solution
We can see the graph of g is the graph of ![]() shifted to the left 2 and down 3, giving a formula in the form
shifted to the left 2 and down 3, giving a formula in the form ![]() .
.
Substituting the coordinates of a point on the curve, such as ![]() we can solve for the stretch factor.
we can solve for the stretch factor.
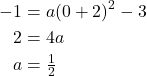
In standard form, the algebraic model for this graph is ![]() .
.
To write this in general polynomial form, we can expand the formula and simplify terms.
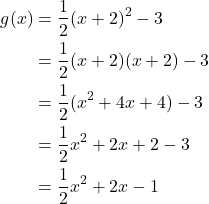
Notice that the horizontal and vertical shifts of the basic graph of the quadratic function determine the location of the vertex of the parabola; the vertex is unaffected by stretches and compressions.
Try It
A coordinate grid has been superimposed over the quadratic path of a basketball. Find an equation for the path of the ball. Does the shooter make the basket?

Show Solution
The path passes through the origin and has vertex at ![]() so
so ![]() To make the shot,
To make the shot, ![]() would need to be about 4 but
would need to be about 4 but ![]() he doesn’t make it.
he doesn’t make it.
How To
Given a quadratic function in general form, find the vertex of the parabola.
- Identify
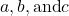 .
. - Find
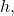 the x-coordinate of the vertex, by substituting
the x-coordinate of the vertex, by substituting  and
and 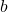 into
into 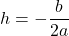 .
. - Find
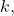 the y-coordinate of the vertex, by evaluating
the y-coordinate of the vertex, by evaluating 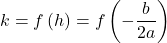 .
.
Finding the Vertex of a Quadratic Function
Find the vertex of the quadratic function ![]() Rewrite the quadratic in standard form (vertex form).
Rewrite the quadratic in standard form (vertex form).
Show Solution

Rewriting into standard form, the stretch factor will be the same as the ![]() in the original quadratic. First, find the horizontal coordinate of the vertex. Then find the vertical coordinate of the vertex. Substitute the values into standard form, using the “
in the original quadratic. First, find the horizontal coordinate of the vertex. Then find the vertical coordinate of the vertex. Substitute the values into standard form, using the “![]() ” from the general form.
” from the general form.
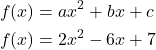
The standard form of a quadratic function prior to writing the function then becomes the following:
Analysis
One reason we may want to identify the vertex of the parabola is that this point will inform us where the maximum or minimum value of the output occurs, ![]() and where it occurs,
and where it occurs, ![]() .
.
Try It
Given the equation ![]() write the equation in general form and then in standard form.
write the equation in general form and then in standard form.
Show Solution
![]() in general form;
in general form; ![]() in standard form
in standard form
Finding the Domain and Range of a Quadratic Function
Any number can be the input value of a quadratic function. Therefore, the domain of any quadratic function is all real numbers. Because parabolas have a maximum or a minimum point, the range is restricted. Since the vertex of a parabola will be either a maximum or a minimum, the range will consist of all y-values greater than or equal to the y-coordinate at the turning point or less than or equal to the y-coordinate at the turning point, depending on whether the parabola opens up or down.
Domain and Range of a Quadratic Function
The domain of any quadratic function is all real numbers unless the context of the function presents some restrictions.
The range of a quadratic function written in general form ![]() with a positive
with a positive ![]() value is
value is ![]() or
or ![]() the range of a quadratic function written in general form with a negative
the range of a quadratic function written in general form with a negative ![]() value is
value is ![]() or
or ![]() .
.
The range of a quadratic function written in standard form ![]() with a positive
with a positive ![]() value is
value is ![]() the range of a quadratic function written in standard form with a negative
the range of a quadratic function written in standard form with a negative ![]() value is
value is ![]() .
.
How To
Given a quadratic function, find the domain and range.
- Identify the domain of any quadratic function as all real numbers.
- Determine whether
 is positive or negative. If
is positive or negative. If  is positive, the parabola has a minimum. If
is positive, the parabola has a minimum. If  is negative, the parabola has a maximum.
is negative, the parabola has a maximum. - Determine the maximum or minimum value of the parabola,
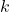 .
. - If the parabola has a minimum, the range is given by
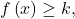 or
or 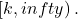 If the parabola has a maximum, the range is given by
If the parabola has a maximum, the range is given by 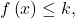 or
or ![Rendered by QuickLaTeX.com \left(-infty ,k \right]](https://utsa.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-2bb8e29e40bb38798e859c8852c490f7_l3.png) .
.
Finding the Domain and Range of a Quadratic Function
Find the domain and range of ![]() .
.
Show Solution
As with any quadratic function, the domain is all real numbers.
Because ![]() is negative, the parabola opens downward and has a maximum value. We need to determine the maximum value. We can begin by finding the
is negative, the parabola opens downward and has a maximum value. We need to determine the maximum value. We can begin by finding the ![]() value of the vertex.
value of the vertex.
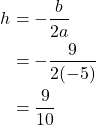
The maximum value is given by ![]() .
.
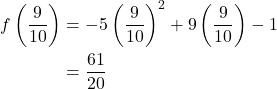
The range is ![]() or
or ![]() .
.
Determining the Maximum and Minimum Values of Quadratic Functions
The output of the quadratic function at the vertex is the maximum or minimum value of the function, depending on the orientation of the parabola. We can see the maximum and minimum values.

There are many real-world scenarios that involve finding the maximum or minimum value of a quadratic function, such as applications involving area and revenue.
Finding the Maximum Value of a Quadratic Function
A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.
- Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length
 .
. - What dimensions should she make her garden to maximize the enclosed area?
Show Solution
Let’s use a diagram to record the given information. It is also helpful to introduce a temporary variable, ![]() to represent the width of the garden and the length of the fence section parallel to the backyard fence.
to represent the width of the garden and the length of the fence section parallel to the backyard fence.

- We know we have only 80 feet of fence available, and
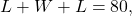 or more simply,
or more simply, 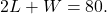 This allows us to represent the width,
This allows us to represent the width, 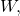 in terms of
in terms of 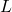 .
.
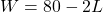
Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so

This formula represents the area of the fence in terms of the variable length
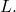 The function, written in general form, is
The function, written in general form, is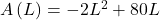 .
. - The quadratic has a negative leading coefficient, so the graph will open downward, and the vertex will be the maximum value for the area. In finding the vertex, we must be careful because the equation is not written in standard polynomial form with decreasing powers. This is why we rewrote the function in general form above. Since
 is the coefficient of the squared term,
is the coefficient of the squared term, 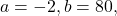 and
and 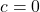 .
.
To find the vertex:
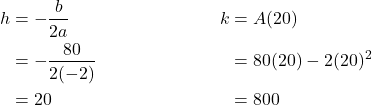
The maximum value of the function is an area of 800 square feet, which occurs when ![]() feet. When the shorter sides are 20 feet, there is 40 feet of fencing left for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet and the longer side parallel to the existing fence has length 40 feet.
feet. When the shorter sides are 20 feet, there is 40 feet of fencing left for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet and the longer side parallel to the existing fence has length 40 feet.
Analysis
This problem also could be solved by graphing the quadratic function. We can see where the maximum area occurs on a graph of the quadratic function.

Applying the Vertex and x-Intercepts of a Parabola
A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation ![]() .
.
- When does the ball reach the maximum height?
- What is the maximum height of the ball?
- When does the ball hit the ground?
Show Solution
- The ball reaches the maximum height at the vertex of the parabola.
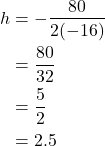
The ball reaches a maximum height after 2.5 seconds.
- To find the maximum height, find the
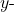 coordinate of the vertex of the parabola.
coordinate of the vertex of the parabola.
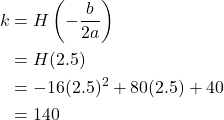
The ball reaches a maximum height of 140 feet.
- To find when the ball hits the ground, we need to determine when the height is zero,
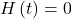 .We use the quadratic formula.
.We use the quadratic formula.
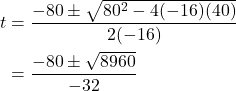
Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.
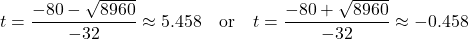
The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds.

Note that the graph does not represent the physical path of the ball upward and downward. Keep the quantities on each axis in mind while interpreting the graph.
Try It
A rock is thrown upward from the top of a 112-foot high cliff overlooking the ocean at a speed of 96 feet per second. The rock’s height above ocean can be modeled by the equation ![]() .
.
- When does the rock reach the maximum height?
- What is the maximum height of the rock?
- When does the rock hit the ocean?
Show Solution
3 seconds256 feet7 seconds
Access these online resources for additional instruction and practice with quadratic equations.
Key Concepts
- A polynomial function of degree two is called a quadratic function.
- The graph of a quadratic function is a parabola. A parabola is a U-shaped curve that can open either up or down.
- The axis of symmetry is the vertical line passing through the vertex. The zeros, or
 intercepts, are the points at which the parabola crosses the
intercepts, are the points at which the parabola crosses the 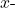 axis. The
axis. The 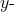 intercept is the point at which the parabola crosses the
intercept is the point at which the parabola crosses the 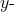 axis.
axis. - Quadratic functions are often written in general form. Standard or vertex form is useful to easily identify the vertex of a parabola. Either form can be written from a graph.
- The vertex can be found from an equation representing a quadratic function.
- The domain of a quadratic function is all real numbers. The range varies with the function.
- A quadratic function’s minimum or maximum value is given by the
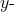 value of the vertex.
value of the vertex. - The minimum or maximum value of a quadratic function can be used to determine the range of the function and to solve many kinds of real-world problems, including problems involving area and revenue.
- The vertex and the intercepts can be identified and interpreted to solve real-world problems.

