Learning Module 01A – Algebraic Essentials & Linear Equations
The Rectangular Coordinate Systems and Graphs
Learning Objectives
In this section you will:
- Plot ordered pairs in a Cartesian coordinate system.
- Graph equations by plotting points.
- Find
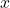 -intercepts and
-intercepts and 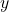 -intercepts.
-intercepts.

Tracie set out from Elmhurst, IL, to go to Franklin Park. On the way, she made a few stops to do errands. Each stop is indicated by a red dot in image above. Laying a rectangular coordinate grid over the map, we can see that each stop aligns with an intersection of grid lines. In this section, we will learn how to use grid lines to describe locations and changes in locations.
Plotting Ordered Pairs in the Cartesian Coordinate System
An old story describes how seventeenth-century philosopher/mathematician René Descartes invented the system that has become the foundation of algebra while sick in bed. According to the story, Descartes was staring at a fly crawling on the ceiling when he realized that he could describe the fly’s location in relation to the perpendicular lines formed by the adjacent walls of his room. He viewed the perpendicular lines as horizontal and vertical axes. Further, by dividing each axis into equal unit lengths, Descartes saw that it was possible to locate any object in a two-dimensional plane using just two numbers—the displacement from the horizontal axis and the displacement from the vertical axis.
While there is evidence that ideas similar to Descartes’ grid system existed centuries earlier, it was Descartes who introduced the components that comprise the Cartesian coordinate system, a grid system having perpendicular axes. Descartes named the horizontal axis the x-axis and the vertical axis the y-axis.
The Cartesian coordinate system, also called the rectangular coordinate system, is based on a two-dimensional plane consisting of the x-axis and the y-axis. Perpendicular to each other, the axes divide the plane into four sections. Each section is called a quadrant; the quadrants are numbered counterclockwise as shown in the graph below.

The center of the plane is the point at which the two axes cross. It is known as the origin, or point ![]() . From the origin, each axis is further divided into equal units: increasing, positive numbers to the right on the x-axis and up the y-axis; decreasing, negative numbers to the left on the x-axis and down the y-axis. The axes extend to positive and negative infinity as shown by the arrowheads in the graph below.
. From the origin, each axis is further divided into equal units: increasing, positive numbers to the right on the x-axis and up the y-axis; decreasing, negative numbers to the left on the x-axis and down the y-axis. The axes extend to positive and negative infinity as shown by the arrowheads in the graph below.

Each point in the plane is identified by its x-coordinate, or horizontal displacement from the origin, and its y-coordinate, or vertical displacement from the origin. Together, we write them as an ordered pair indicating the combined distance from the origin in the form, ![]() . An ordered pair is also known as a coordinate pair because it consists of x- and y-coordinates. For example, we can represent the point,
. An ordered pair is also known as a coordinate pair because it consists of x- and y-coordinates. For example, we can represent the point, ![]() , in the plane by moving three units to the right of the origin in the horizontal direction, and one unit down in the vertical direction.
, in the plane by moving three units to the right of the origin in the horizontal direction, and one unit down in the vertical direction.

When dividing the axes into equally spaced increments, note that the x-axis may be considered separately from the y-axis. In other words, while the x-axis may be divided and labeled according to consecutive integers, the y-axis may be divided and labeled by increments of 2, or 10, or 100. In fact, the axes may represent other units, such as years against the balance in a savings account, or quantity against cost, and so on. Consider the rectangular coordinate system primarily as a method for showing the relationship between two quantities.
Cartesian Coordinate System
A two-dimensional plane where the
- x-axis is the horizontal axis
- y-axis is the vertical axis
A point in the plane is defined as an ordered pair, ![]() such that x is determined by its horizontal distance from the origin and y is determined by its vertical distance from the origin.
such that x is determined by its horizontal distance from the origin and y is determined by its vertical distance from the origin.
Plotting Points in a Rectangular Coordinate System
Plot the points![]()
![]() and
and![]() in the plane.
in the plane.
Show Solution
To plot the point, ![]() , begin at the origin. The x-coordinate is –2, so move two units to the left. The y-coordinate is 4, so then move four units up in the positive y direction.
, begin at the origin. The x-coordinate is –2, so move two units to the left. The y-coordinate is 4, so then move four units up in the positive y direction.
To plot the point, ![]() , begin again at the origin. The x-coordinate is 3, so move three units to the right. The y-coordinate is also 3, so move three units up in the positive y direction.
, begin again at the origin. The x-coordinate is 3, so move three units to the right. The y-coordinate is also 3, so move three units up in the positive y direction.
To plot the point ![]() begin again at the origin. The x-coordinate is 0. This tells us not to move in either direction along the x-axis. The y-coordinate is –3, so move three units down in the negative y direction.
begin again at the origin. The x-coordinate is 0. This tells us not to move in either direction along the x-axis. The y-coordinate is –3, so move three units down in the negative y direction.

Analysis
Note that when either coordinate is zero, the point must be on an axis. If the x-coordinate is zero, the point is on the y-axis. If the y-coordinate is zero, the point is on the x-axis.
Graphing Equations by Plotting Points
We can plot a set of points to represent an equation. When such an equation contains both an x variable and a y variable, it is called an equation in two variables. Its graph is called a graph in two variables. Any graph on a two-dimensional plane is a graph in two variables.
Suppose we want to graph the equation ![]() . We can begin by substituting a value for x into the equation and determining the resulting value of y. Each pair of x– and y-values is an ordered pair that can be plotted. The table below lists values of x from –3 to 3 and the resulting values for y.
. We can begin by substituting a value for x into the equation and determining the resulting value of y. Each pair of x– and y-values is an ordered pair that can be plotted. The table below lists values of x from –3 to 3 and the resulting values for y.
We can plot the points in the table. The points for this particular equation form a line, so we can connect them. This is not true for all equations.
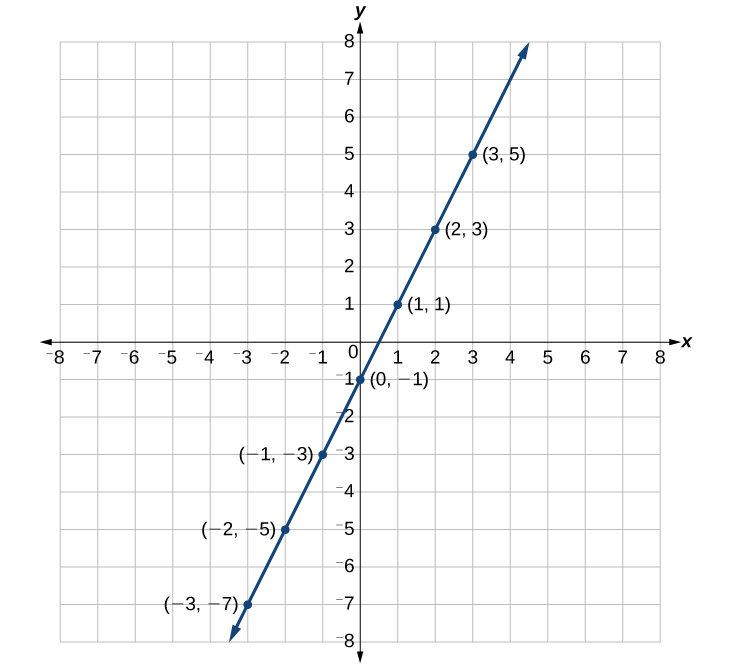
Note that the x-values chosen are arbitrary, regardless of the type of equation we are graphing. Of course, some situations may require particular values of x to be plotted in order to see a particular result. Otherwise, it is logical to choose values that can be calculated easily, and it is always a good idea to choose values that are both negative and positive. There is no rule dictating how many points to plot, although we need at least two to graph a line. Keep in mind, however, that the more points we plot, the more accurately we can sketch the graph.
How To
Given an equation, graph by plotting points.
- Make a table with one column labeled x, a second column labeled with the equation, and a third column listing the resulting ordered pairs.
- Enter x-values down the first column using positive and negative values. Selecting the x-values in numerical order will make the graphing simpler.
- Select x-values that will yield y-values with little effort, preferably ones that can be calculated mentally.
- Plot the ordered pairs.
- Connect the points if they form a line.
Graphing an Equation in Two Variables by Plotting Points
Graph the equation ![]() by plotting points.
by plotting points.
Show Solution
First, we construct a table. Choose x values and calculate y.
Now, plot the points. Connect them if they form a line.

Try It
Construct a table and graph the equation by plotting points: ![]()
Show Solution

The intercepts of a graph are points at which the graph crosses the axes. The x-intercept is the point at which the graph crosses the x-axis. At this point, the y-coordinate is zero. The y-intercept is the point at which the graph crosses the y-axis. At this point, the x-coordinate is zero.
To determine the x-intercept, we set y equal to zero and solve for x. Similarly, to determine the y-intercept, we set x equal to zero and solve for y. For example, lets find the intercepts of the equation ![]()
To find the x-intercept, set ![]()
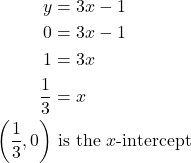
To find the y-intercept, set ![]()
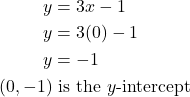
We can confirm that our results make sense by observing a graph of the equation. Notice that the graph crosses the axes where we predicted it would.

How To
Given an equation, find the intercepts.
- Find the x-intercept by setting
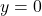 and solving for
and solving for  .
. - Find the y-intercept by setting
 and solving for
and solving for 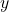 .
.
Finding the Intercepts of the Given Equation
Find the intercepts of the equation ![]() Then sketch the graph using only the intercepts.
Then sketch the graph using only the intercepts.
Show Solution
Set ![]() to find the x-intercept.
to find the x-intercept.
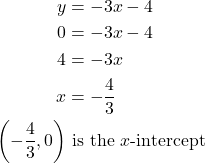
Set ![]() to find the y-intercept.
to find the y-intercept.
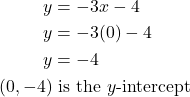
Plot both points, and draw a line passing through them.

Try It
Find the intercepts of the equation and sketch the graph: ![]() .
.
Show Solution
x-intercept is ![]() y-intercept is
y-intercept is ![]()

Access these online resources for additional instruction and practice with the Cartesian coordinate system.
Key Concepts
- We can locate, or plot, points in the Cartesian coordinate system using ordered pairs, which are defined as displacement from the x-axis and displacement from the y-axis.
- An equation can be graphed in the plane by creating a table of values and plotting points.
- Using a graphing calculator or a computer program makes graphing equations faster and more accurate. Equations usually have to be entered in the form y=_____.
- Finding the x- and y-intercepts can define the graph of a line. These are the points where the graph crosses the axes.

