Learning Module 07A Rational Expressions & Equations
Rational Expressions and Equations
Learning Objectives
In this section students will:
- Simplify rational expressions.
- Multiply rational expressions.
- Divide rational expressions.
- Add and subtract rational expressions.
- Simplify complex rational expressions.
- Rationalize a denominator.
- Solve a linear rational equation.
- Determine the domain of rational equations.
A pastry shop has fixed costs of ![]() per week and variable costs of
per week and variable costs of ![]() per box of pastries. The shop’s costs per week in terms of
per box of pastries. The shop’s costs per week in terms of ![]() the number of boxes made, is
the number of boxes made, is ![]() We can divide the costs per week by the number of boxes made to determine the cost per box of pastries.
We can divide the costs per week by the number of boxes made to determine the cost per box of pastries.
Notice that the result is a polynomial expression divided by a second polynomial expression. In this section, we will explore quotients of polynomial expressions.
Simplifying Rational Expressions
The quotient of two polynomial expressions is called a rational expression. We can apply the properties of fractions to rational expressions, such as simplifying the expressions by canceling common factors from the numerator and the denominator. To do this, we first need to factor both the numerator and denominator. Let’s start with the rational expression shown.
We can factor the numerator and denominator to rewrite the expression.
Then we can simplify that expression by canceling the common factor ![]() .
.
How To
Given a rational expression, simplify it.
- Factor the numerator and denominator.
- Cancel any common factors.
Simplifying Rational Expressions
Simplify ![]() .
.
Show Solution

Analysis
We can cancel the common factor because any expression divided by itself is equal to 1.
Multiplying Rational Expressions
Multiplication of rational expressions works the same way as multiplication of any other fractions. We multiply the numerators to find the numerator of the product, and then multiply the denominators to find the denominator of the product. Before multiplying, it is helpful to factor the numerators and denominators just as we did when simplifying rational expressions. We are often able to simplify the product of rational expressions.
How To
Given two rational expressions, multiply them.
- Factor the numerator and denominator.
- Multiply the numerators.
- Multiply the denominators.
- Simplify.
Multiplying Rational Expressions
Multiply the rational expressions and show the product in simplest form:
Show Solution

Dividing Rational Expressions
Division of rational expressions works the same way as division of other fractions. To divide a rational expression by another rational expression, multiply the first expression by the reciprocal of the second. Using this approach, we would rewrite ![]() as the product
as the product ![]() Once the division expression has been rewritten as a multiplication expression, we can multiply as we did before.
Once the division expression has been rewritten as a multiplication expression, we can multiply as we did before.
How To
Given two rational expressions, divide them.
- Rewrite as the first rational expression multiplied by the reciprocal of the second.
- Factor the numerators and denominators.
- Multiply the numerators.
- Multiply the denominators.
- Simplify.
Dividing Rational Expressions
Divide the rational expressions and express the quotient in simplest form:
Show Solution
Adding and Subtracting Rational Expressions
Adding and subtracting rational expressions works just like adding and subtracting numerical fractions. To add fractions, we need to find a common denominator. Let’s look at an example of fraction addition.

We have to rewrite the fractions so they share a common denominator before we are able to add. We must do the same thing when adding or subtracting rational expressions.
The easiest common denominator to use will be the least common denominator, or LCD. The LCD is the smallest multiple that the denominators have in common. To find the LCD of two rational expressions, we factor the expressions and multiply all of the distinct factors. For instance, if the factored denominators were ![]() and
and ![]() then the LCD would be
then the LCD would be ![]() .
.
Once we find the LCD, we need to multiply each expression by the form of 1 that will change the denominator to the LCD. We would need to multiply the expression with a denominator of ![]() by
by ![]() and the expression with a denominator of
and the expression with a denominator of ![]() by
by ![]() .
.
How To
Given two rational expressions, add or subtract them.
- Factor the numerator and denominator.
- Find the LCD of the expressions.
- Multiply the expressions by a form of 1 that changes the denominators to the LCD.
- Add or subtract the numerators.
- Simplify.
Adding Rational Expressions
Add the rational expressions:
Show Solution
First, we have to find the LCD. In this case, the LCD will be ![]() We then multiply each expression by the appropriate form of 1 to obtain
We then multiply each expression by the appropriate form of 1 to obtain ![]() as the denominator for each fraction.
as the denominator for each fraction.

Now that the expressions have the same denominator, we simply add the numerators to find the sum.
Analysis
Multiplying by ![]() or
or ![]() does not change the value of the original expression because any number divided by itself is 1, and multiplying an expression by 1 gives the original expression.
does not change the value of the original expression because any number divided by itself is 1, and multiplying an expression by 1 gives the original expression.
Simplifying Complex Rational Expressions
A complex rational expression is a rational expression that contains additional rational expressions in the numerator, the denominator, or both. We can simplify complex rational expressions by rewriting the numerator and denominator as single rational expressions and dividing. The complex rational expression ![]() can be simplified by rewriting the numerator as the fraction
can be simplified by rewriting the numerator as the fraction ![]() and combining the expressions in the denominator as
and combining the expressions in the denominator as ![]() We can then rewrite the expression as a multiplication problem using the reciprocal of the denominator. We get
We can then rewrite the expression as a multiplication problem using the reciprocal of the denominator. We get ![]() which is equal to
which is equal to ![]() .
.
How To
Given a complex rational expression, simplify it.
- Combine the expressions in the numerator into a single rational expression by adding or subtracting.
- Combine the expressions in the denominator into a single rational expression by adding or subtracting.
- Rewrite as the numerator divided by the denominator.
- Rewrite as multiplication.
- Multiply.
- Simplify.
Simplifying Complex Rational Expressions
Simplify:![]() .
.
Show Solution
Begin by combining the expressions in the numerator into one expression.
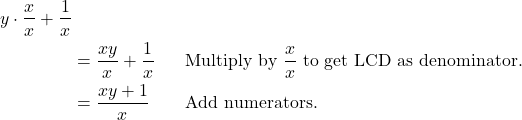
Now the numerator is a single rational expression and the denominator is a single rational expression.
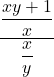
We can rewrite this as division, and then multiplication.
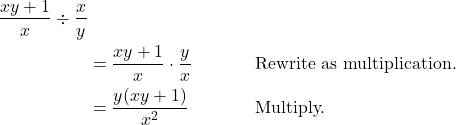
Can a complex rational expression always be simplified?
Yes. We can always rewrite a complex rational expression as a simplified rational expression.
Rationalizing Denominators
When an expression involving square root radicals is written in simplest form, it will not contain a radical in the denominator. We can remove radicals from the denominators of fractions using a process called rationalizing the denominator.
We know that multiplying by 1 does not change the value of an expression. We use this property of multiplication to change expressions that contain radicals in the denominator. To remove radicals from the denominators of fractions, multiply by the form of 1 that will eliminate the radical.
For a denominator containing a single term, multiply by the radical in the denominator over itself. In other words, if the denominator is ![]() multiply by
multiply by ![]()
For a denominator containing the sum or difference of a rational and an irrational term, multiply the numerator and denominator by the conjugate of the denominator, which is found by changing the sign of the radical portion of the denominator. If the denominator is ![]() then the conjugate is
then the conjugate is ![]()
How To
Given an expression with a single square root radical term in the denominator, rationalize the denominator.
- Multiply the numerator and denominator by the radical in the denominator.
- Simplify.
Rationalizing a Denominator Containing a Single Term
Write ![]() in simplest form.
in simplest form.
Show Solution
The radical in the denominator is ![]() So multiply the fraction by
So multiply the fraction by ![]() Then simplify.
Then simplify.
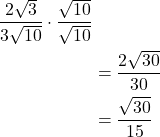
Try It
Write ![]() in simplest form.
in simplest form.
Show Solution
![]()
How To
Given an expression with a radical term and a constant in the denominator, rationalize the denominator.
- Find the conjugate of the denominator.
- Multiply the numerator and denominator by the conjugate.
- Use the distributive property.
- Simplify.
Rationalizing a Denominator Containing Two Terms
Write ![]() in simplest form.
in simplest form.
Show Solution
Begin by finding the conjugate of the denominator by writing the denominator and changing the sign. So the conjugate of ![]() is
is ![]() Then multiply the fraction by
Then multiply the fraction by ![]()
![]()
Try It
Write ![]() in simplest form.
in simplest form.
Show Solution
![]()
Solving a Linear Rational Equation
In this section, we look at rational equations that, after some manipulation, result in a linear equation. If an equation contains at least one rational expression, it is a considered a rational equation.
Recall that a rational number is the ratio of two numbers, such as ![]() or
or ![]() . A rational expression is the ratio, or quotient, of two polynomials. Here are three examples:
. A rational expression is the ratio, or quotient, of two polynomials. Here are three examples:
Rational equations have a variable in the denominator in at least one of the terms.
Our goal is to perform algebraic operations so that the variables appear in the numerator. In fact, we will eliminate all denominators by multiplying both sides of the equation by the least common denominator (LCD).
Finding the LCD is identifying an expression that contains the highest power of all of the factors in all of the denominators. We do this because when the equation is multiplied by the LCD, the common factors in the LCD and in each denominator will equal one and will cancel out.
Solving a Rational Equation
Solve the rational equation: ![]()
Show Solution
First, let’s determine the LCD. We have three denominators: ![]()
![]() and
and ![]() . The LCD must contain
. The LCD must contain ![]()
![]() and
and ![]() . An LCD of
. An LCD of ![]() contains all three denominators. In other words, each denominator can be divided evenly into the LCD.
contains all three denominators. In other words, each denominator can be divided evenly into the LCD.
Next, we multiply both sides of the equation by the LCD ![]() . Since we are multiplying a whole number by a fraction, we can rewrite the whole number as an equivalent fraction:
. Since we are multiplying a whole number by a fraction, we can rewrite the whole number as an equivalent fraction: ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
We can cancel common factors in the numerator and denominator to clear the fractions:
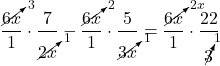
![]()
![]()
Now, we can solve for the value of ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A common mistake made when solving rational equations involves finding the LCD when one of the denominators is a binomial—two terms added or subtracted—such as ![]() . Always consider a binomial as an individual factor—the terms cannot be separated. For example, suppose a problem has three terms and the denominators are
. Always consider a binomial as an individual factor—the terms cannot be separated. For example, suppose a problem has three terms and the denominators are ![]()
![]() and
and ![]() . First, factor all denominators. We then have
. First, factor all denominators. We then have ![]()
![]() and
and ![]() as the denominators. (Note the parentheses placed around the second denominator.) Only the last two denominators have a common factor of
as the denominators. (Note the parentheses placed around the second denominator.) Only the last two denominators have a common factor of ![]() . The
. The ![]() in the first denominator is separate from the
in the first denominator is separate from the ![]() in the
in the ![]() denominators. An effective way to remember this is to write factored and binomial denominators in parentheses and consider each parenthesis as a separate unit or a separate factor. The LCD in this instance is found by multiplying together the
denominators. An effective way to remember this is to write factored and binomial denominators in parentheses and consider each parenthesis as a separate unit or a separate factor. The LCD in this instance is found by multiplying together the ![]() one factor of
one factor of ![]() and the 3. Thus, the LCD is the following:
and the 3. Thus, the LCD is the following:
So, both sides of the equation would be multiplied by ![]() . Leave the LCD in factored form, as this makes it easier to see how each denominator in the problem cancels out.
. Leave the LCD in factored form, as this makes it easier to see how each denominator in the problem cancels out.
Another example is a problem with two denominators, such as ![]() and
and ![]() . Once the second denominator is factored as
. Once the second denominator is factored as ![]() there is a common factor of x in both denominators and the LCD is
there is a common factor of x in both denominators and the LCD is ![]() .
.
Sometimes we have a rational equation in the form of a proportion; that is, when one \dfraction equals another \dfraction and there are no other terms in the equation.
We can use another method of solving the equation without finding the LCD: cross-multiplication. We multiply terms by crossing over the equal sign.

Multiply ![]() and
and ![]() which results in
which results in ![]()
Any solution that makes a denominator in the original expression equal zero must be excluded from the possibilities.
Rational Equations
A rational equation contains at least one rational expression where the variable appears in at least one of the denominators.
How To
Given a rational equation, solve it.
- Factor all denominators in the equation.
- Find and exclude values that set each denominator equal to zero.
- Find the LCD.
- Multiply the whole equation by the LCD. If the LCD is correct, there will be no denominators left.
- Solve the remaining equation.
- Make sure to check solutions back in the original equations to avoid a solution producing zero in a denominator
Solving a Rational Equation without Factoring
Solve the following rational equation:
Show Solution
We have three denominators: ![]() ,
, ![]() , and,
, and, ![]() . No factoring is required. The product of the first two denominators is equal to the third denominator, so, the LCD is
. No factoring is required. The product of the first two denominators is equal to the third denominator, so, the LCD is ![]() . Only one value is excluded from a solution set
. Only one value is excluded from a solution set ![]() . Next, multiply the whole equation (both sides of the equal sign) by
. Next, multiply the whole equation (both sides of the equal sign) by ![]() .
.
![]()
![]()
![]()
![]()
The proposed solution is ![]() which is not an excluded value, so the solution set contains one number,
which is not an excluded value, so the solution set contains one number, ![]() .
.
Try It
Solve the rational equation: ![]()
Show Solution
![]()
Solving a Rational Equation by Factoring the Denominator
Solve the following rational equation: ![]()
Show Solution
First find the common denominator. The three denominators in factored form are ![]()
![]() and
and ![]() . The smallest expression that is divisible by each one of the denominators is
. The smallest expression that is divisible by each one of the denominators is ![]() . Only
. Only ![]() is an excluded value. Multiply the whole equation by
is an excluded value. Multiply the whole equation by ![]() .
.
![]()
The solution is ![]() .
.
Try It
Solve the rational equation:![]()
Show Solution
![]()
Solving Rational Equations with a Binomial in the Denominator
Solve the following rational equations and state the excluded values:
Show Solution
- The denominators
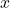 and
and 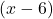 have nothing in common. Therefore, the LCD is the product
have nothing in common. Therefore, the LCD is the product 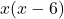 . However, for this problem, we can cross-multiply.
. However, for this problem, we can cross-multiply.
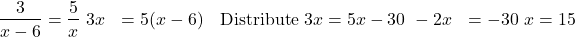
The solution is
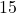 . The excluded values are
. The excluded values are 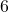 and
and 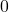
- The LCD is
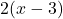 . Multiply both sides of the equation by
. Multiply both sides of the equation by 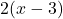 .
.
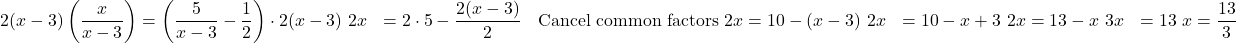
The solution is
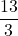 . The excluded value is
. The excluded value is 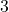 .
. - The least common denominator is
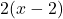 . Multiply both sides of the equation by
. Multiply both sides of the equation by 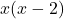 .
.
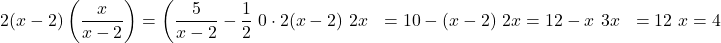
The solution is
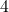 . The excluded value is
. The excluded value is 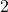 /
/
Try It
Solve ![]() . State the excluded values.
. State the excluded values.
Show Solution
![]() . Excluded values are
. Excluded values are ![]() and
and ![]() .
.
Solving a Rational Equation with Factored Denominators and Stating Excluded Values
Solve the rational equation after factoring the denominators: ![]() . State the excluded values.
. State the excluded values.
Show Solution
We must factor the denominator ![]() . We recognize this as the difference of squares, and factor it as
. We recognize this as the difference of squares, and factor it as![]() Thus, the LCD that contains each denominator is
Thus, the LCD that contains each denominator is![]() Multiply the whole equation by the LCD, cancel out the denominators, and solve the remaining equation.
Multiply the whole equation by the LCD, cancel out the denominators, and solve the remaining equation.
![]()
The solution is ![]() . The excluded values are
. The excluded values are ![]() and
and ![]() .
.
Try It
Solve the rational equation:![]()
Show Solution
![]()
Determining the Domain of Rational Equations
Recall that we cannot include any input value in the domain that would lead us to divide by 0. When we are working with rational equations or rational functions, we must exclude values from the denominator that will result in division by 0.
How To
Given a function written in an equation form that includes a fraction, find the domain.
- Identify the input values.
- Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for
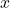 . If the function’s formula contains an even root, set the radicand greater than or equal to 0, and then solve.
. If the function’s formula contains an even root, set the radicand greater than or equal to 0, and then solve. - Write the domain in interval form, making sure to exclude any restricted values from the domain.
Finding the Domain of a Function Involving a Denominator
Find the domain of the function ![]() .
.
Show Solution
When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for ![]() .
.
![]()
Now, we will exclude 2 from the domain. The answers are all real numbers where ![]() or
or ![]() as shown below. We can use a symbol known as the union,
as shown below. We can use a symbol known as the union, ![]() to combine the two sets. In interval notation, we write the solution:
to combine the two sets. In interval notation, we write the solution: ![]() .
.

Try It
Find the domain of the function: ![]() .
.
Show Solution
![]()
Access these online resources for additional instruction and practice with rational expressions.
Key Concepts
- Rational expressions can be simplified by cancelling common factors in the numerator and denominator.
- We can multiply rational expressions by multiplying the numerators and multiplying the denominators.
- To divide rational expressions, multiply by the reciprocal of the second expression.
- Adding or subtracting rational expressions requires finding a common denominator.
- Complex rational expressions have fractions in the numerator or the denominator. These expressions can be simplified.
- A rational expression is a quotient of two polynomials. We use the LCD to clear the fractions from an equation.
- All solutions to a rational equation should be verified within the original equation to avoid an undefined term, or zero in the denominator.

